Přijímací zkoušky se nezadržitelně blíží. Testy studijních předpokladů jsou specifikem přijímacích zkoušek 2. Lékařské fakulty Univerzity Karlovy. Šest typů úlohy má za úkol otestovat uchazečovo logické uvažování, porozumění textu, schopnost postřehnout detail či jeho prostorovou představivost. Na jaké konkrétní úlohy v nich můžeme narazit a dá se na ně nějakým způsobem připravit předem? Pojďme se na ně podívat a společně i některé z nich vyřešit.
Všechny ukázkové úlohy vychází z testů, které vytvořili lektoři Bmedic (ve stylu TSP 2.LF). Tyto testy je možné získat ZDE.
Porozumění grafům a tabulkám
V tomto typu úloh narážíme na graf či tabulku doplněnou o zadání. Je více variant – buď je po uchazečovi požadována identifikace zobrazované funkce včetně jejího matematického vyjádření (např. že kvadratická funkce má tvar paraboly a je vyjádřena vztahem f(x) = ax2 + bx + c), či musí z řady tvrzení vybrat to správné, které lze z grafu vyčíst, jako na následujícím příkladu:

Výřez grafu znázorňuje kumulativní vývoj zemřelých ve sledované skupině 80 pacientů. Osa x znázorňuje počet přežitých měsíců po diagnóze, osa y zanáší kumulativní počet pacientů, kteří se dožili míň, než počet měsíců na osy x. Vyberte správné tvrzení:
A: Pacientů, kteří se dožili 15 měsíců, bylo 58
B: Víc pacientů zemřelo mezi 15. a 20. měsícem, než mezi 10. a 15. měsícem
C: Pacientů, kteří se dožili 20 měsíců, bylo 5
D: Nejvíc pacientů zemřelo mezi 5. a 10. měsícem
E: Rok a půl po diagnóze žilo 65 pacientů
Je potřeba se v grafu správně zorientovat – kde je a co zobrazuje osa x a osa y a co za údaje vlastně z grafu můžeme vyčíst? Následně můžeme přikročit k potvrzování a vyvracování tvrzení. Možnost A si můžeme škrtnout – graf nám ukazuje vývoj počtu zemřelých, nikoliv těch, kteří se daného měsíce dožili. U tvrzení B porovnáváme nárůst křivky mezi 10. a 15. měsícem a 15. a 20. měsícem. Za využití světle šedých os lze snadno určit, že křivka narostla více v období 10.-15. měsíce, proto můžeme i B vyloučit. Co se týče C, z grafu lze vyčíst, že v 20. měsíci bylo po smrti 70 pacientů. V zadání máme, že celkový počet zkoumaných byl 80, 20. měsíce se jich tedy dožilo 10 – C je tedy taky nepravdivé. V možnosti D hledáme časový úsek, kdy byl nárůst křivky největší, k čemuž nám opět pomůže síť světle šedých os. Zjistíme, že k největší nárůst graf zaznamenal v období 5. až 10. měsíce, D je tedy správně. Pro úplnost si vyvrátíme ještě možnost E, kde musíme trochu zapojit představivost – 18 měsíců přímo na ose x vyznačeno nemáme, určíme si ji tedy přibližně a představíme si, kde by kolmice procházející daným bodem proťala graf. Daný průsečík by odpovídal hodnotě 65 na ose y, ale opět je potřeba si uvědomit, že graf zobrazuje počet zemřelých – naživu jich tedy v 18. měsíci bylo 25, možnost E je tedy špatně.
Pokud si nejste svými schopnosti čtení z grafu jisti, lze je poměrně snadno procvičovat. Stačí zadat do vyhledavače „čtení z grafů“ a vyskočí vám nejedna webová stránka, kde můžete své dovednosti utužovat a procvičovat. Také není od věci si zopakovat již zmíněné funkce – znalosti, jak vypadají a jaký mají předpis, vám mohou přijít vhod.
Celek a výřez
Jak už název napovídá, uchazeč musí v těchto úlohách vybrat z 5 výřezů ten, který se liší od vzorového obrázku. Smyslem je otestovat smysl pro detail. Jde o něco časově náročnější příklady a chvíli zabere, než si člověk projde všech 5 možností a správně identifikuje tu rozdílnou (obzvlášť, když je to až ta 5.), nicméně patří také k těm jednodušším – rozdíl je vždy dostatečně znatelný, nesetkáte se s tím, že by se obrázky lišily o nepatrnou tečku nebo lehké prohnutí křivky.

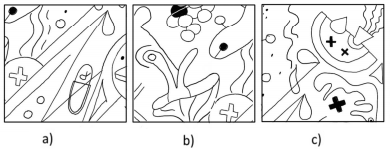

Jako první je samozřejmě potřebovat zjistit, z jaké konkrétní části vzoru je výřez vybrán. Následně je už jen potřeba porovnávat. Nechybí nebo naopak nepřebývá nějaká struktura? Má vše stejnou barvu jako ve vzoru? Je vše ve stejné poloze a stejně orientované (tzn. není něco převrácené)? Pokud si odpovíte na tyto otázky, měli byste nalézt správnou odpověď – v tomto konkrétním příkladu možnost b). Při samotném testu bych se prohlížením dalších obrázků nezdržovala – času není nazbyt. Pokud si budete jisti, že jste rozdíl nalezli v možnosti a), zaškrtněte ji a běžte dál. Kdyby vám přece jen nějaký zbyl, vždy se k příkladu můžete vrátit a zkontrolovat i ostatní možnosti.
Matematické úlohy
Na nějakou tu matematiku jsme narazili už u grafů a některé z vás možná zklamu – v TSP jí je ještě více. Nebojte, nejde o žádné složitosti, jakými jsou třeba integrály, nýbrž spíše o operace, které se během studia medicíny dají využít. Jde především o pravděpodobnost, setkat se ale můžeme i s příklady na ředění podobné těm v chemii a výpočty frekvence alel. Podívejme se na vzorový příklad na pravděpodobnost:
V jistém vzorku populace byla změřena frekvence výskytu modré barvy očí u 20 % lidí. Ve stejném skupině se krevní skupina A vyskytuje u 45 % lidí. S jakou pravděpodobnou četností se v populaci vyskytují lidé s oběma těmito vlastnostmi (zároveň)? Výskyt obou jevů berme jako vzájemně na sobě nezávislý.
a) 0,09 % b) 9 % c) 65 % d) 25 % e) 32,5 %
Příklad spočteme pomocí výpočtu pravděpodobnosti dvou náhodných jevů, tzn. vynásobením. P = 0,2 x 0,45 = 0,09 = 9 %, správně je tedy možnost b). Zde kromě oprášení matematických znalostí moc tipů přidat nelze, opět ale platí, že pokud nevíte, příkladem se nezdržujte a pokračujte dál.
Rozlišení rozdílů
Další typ úloh zkoumající smysl pro detail, tentokrát ale o něco podrobněji. Rozdíly v těchto obrázcích se hledají velmi těžko a člověk je často přesvědčený o tom, že mezi nimi žádný rozdíl není. Opět jde o časově náročnější úlohu. Uchazeč musí vybrat z 5 možností tu, která se nejlépe shoduje se vzorem.
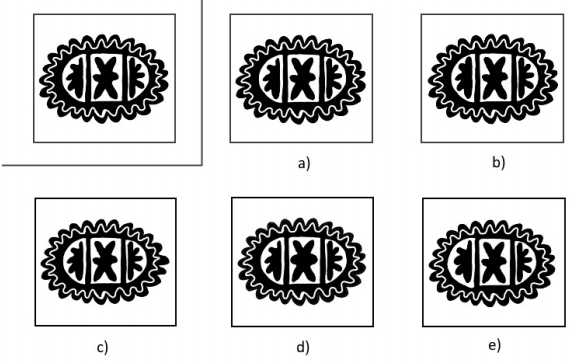
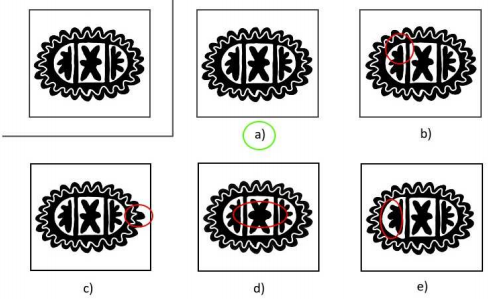
Opět panuje podobná otázka jako u typu „Celek a výřez“ – na co se zaměřit? Ověříme si, zda nám v obrázku nějaká struktura nepřebývá či nechybí. Dále zkontrolujeme, zda mají všechny komponenty stejný tvar, tloušťku a velikost a jsme opravu kritičtí – i malý nepatrný rozdíl je rozdíl. Takto bychom odhalili rozdíly u možností b), c), d) a d).
Logické problémy
V úlohách tohoto typu jde především o schopnost porozumět správně textu. Nejčastěji je vám předložen úvodní text a následně k němu vztažena 3 či více tvrzení. Vaším úkolem je vybrat, která tvrzení vyplývají z textu či které je pravdivé, což možná zní trochu jednoduše, ale často je opak pravdou. Můžete tu totiž občas narazit na lehké slovíčkaření, které vám může pocuchat myšlenkové pochody v hlavě.
Dýchací řetězec se skládá ze 4 enzymových komplexů a enzymu ATP synthasy. Při přenosu elektronů vzniká energie, kterou využívá každý komplex k čerpání protonů z matrix do mezimembránového prostoru. Během přechodu protonů zpět do matrix vzniká energie, která pohání syntézu ATP z ADP a Pi. Protony roztáčí stopku hlavy ATP-synthasy, a tím dochází k syntéze ATP. Jsou dána následující tvrzení:
I: Pi pohání syntézu ATP z ADP v přítomnosti protonů
II: K syntéze ATP je potřeba, aby docházelo k přenosu elektronů
III: Zatímco protony přechází z matrix do mezimembránového prostoru, elektrony postupují naopak
Která z tvrzení vyplývají z textu?
A: Správně je pouze tvrzení I
B: Správně je tvrzení I a II
C: Správně je tvrzení I a III
D: Správně je pouze tvrzení II
E: Žádné z tvrzení není pravdivé
Je potřeba si text přečíst opravdu pořádně a urovnat si v hlavě souvislosti. Následně si tvrzení po tvrzení s textem porovnávat, zda opravdu z textu přímo či logicky vyplývá.
Tvrzení I můžeme označit za špatné – syntézu ATP nám dle textu pohání energie vznikající při přenosu elektronů, nikoliv Pi. Stejný poznatek nám naopak potvrzuje tvrzení II. Tvrzení III nemůžeme řádně potvrdit – nalézáme zde informaci, že protony přecházejí z matrix do mezimembránového prostoru, ale není zde nic konkrétního o směru pohybu elektronů. Správně by tedy byla možnost D.
Do testu, který obdržíte, si můžete psát. Proto se vůbec nebojte podtrhávat důležité pasáže textu, abyste je snadno znovu našli, či si psát poznámky kolem – pokud vám tyto činnosti pomáhají, směle do nich.
Prostorové struktury
A máme tu poslední typ úloh – asi nikoho nepřekvapí, že tyto příklady testují prostorovou představivost. Nejčastěji jde o z různých úhlů nafocené stavby z kostek nebo průhlednou krabici plnou různého harampádí, přičemž úkolem je správně určit, na které z fotografií se struktura liší od vzorové, případně z jakého úhlu je vyfocena.

A: pohled zprava B: pohled zleva C: pohled shora D: pohled zezadu E: pohled zdola
Je dobré se zaměřit na jednu výraznější strukturu a podle té se orientovat. Zde se jako vhodná jeví červená poklička, která je dominantní částí pravého obrázku, u kterého máme určit, z jaké strany je oproti vzoru zobrazen. Zepředu vidíme, že poklička je v horní části krychle, což už napovídá, že by vpravo mohl být záběr shora. Domněnku si potvrdíme okolními útvary, například orientací bílé hadice, tenisovým míčkem či modrým balonem.
Další tipy
Úlohy jsme si představili, od každé i jednu vzorovou vyřešili a přidali si pár tipů k jejich řešení. Co dalšího by vám mohlo pomoci s vypracováním testu TSP? Především bych znovu upozornila na časový limit – je opravdu šibeniční a většina lidí má tu zkušenost, že test nestíhali vyplnit. Navíc je člověk po testu z biologie, chemie a fyziky už trochu unavený a mysl není tak svěží jako ráno. Proto se opravdu nezdržujte otázkami, u kterých nevíte, jak je vyřešit, a upřednostněte ty, u nichž víte nebo alespoň tušíte, jak na ně. Dále nenechávejte záznamový arch s odpověďmi prázdný – za špatnou odpověď se body neodečítají, za správnou naopak získáváte 3 – tam, kde nevíte, se vyplatí tipovat. Taky bych neplýtvala časem procházením testů studijních předpokladů např. od SCIO apod., od TSP na 2. LF se poměrně liší. Naopak bych doporučila projít si vzorové testy TSP přímo na stránkách fakulty nebo testy, které vytvořili lektoři Bmedic.
Na závěr bych všem ráda popřála hodně štěstí nejen u přijímacích zkoušek na 2. LF, ale i na ostatní fakulty a univerzity. Už zbývá jen pár týdnů usilovné práce a budete si moct vychutnat zasloužené, dlouhé prázdniny. Ty si opravdu doporučuji užít, protože medicína vám už potom jen tak nedá spát. 🙂


